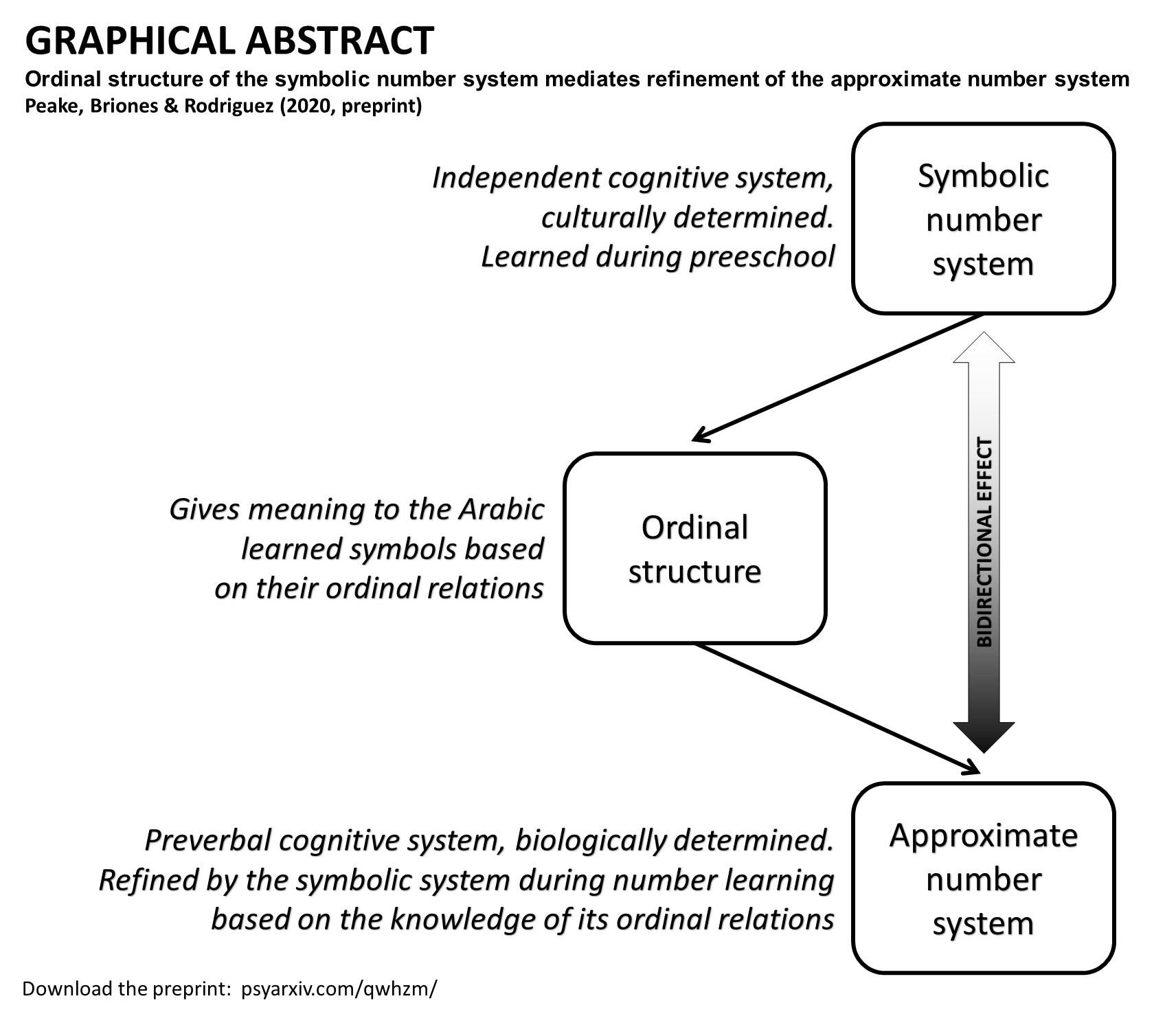
One of the main debates in numerical cognition – a growing body of research framed in cognitive developmental psychology – is how Symbolic Number System (SNS) is acquired and developed and how this development is related to the Approximate Number System (ANS), the so called Symbol Grounding Problem (Harnad, 1990; Leibovich & Ansari, 2016; Reynvoet & Sasanguie, 2016). It should be noted that ANS is approximate in nature, while SNS allows us to represent exact quantities (Ansari, 2008), shown to be a stronger predictor for arithmetic, that is, calculations with exact quantities (Schneider et al., 2017). The traditional view offered a parsimonious developmental explanation of the phenomena (called Mapping Account): as ANS is a biologically determined preverbal early cognitive system and SNS is a culturally developed system that must be acquired through neurofunctional specialization, SNS must rely on ANS during number learning. Thus, we can define number learning as mapping number symbols onto abstract numerical representations (Dehaene, 2011). In the last 15 years, researchers on numerical cognition have proposed an alternative explanation (Carey, 2004), the so-called Parallel Development Account: the SNS could be an independent cognitive system which spontaneously emerges thanks to a bootstrapping process that results in a qualitative different system from the ANS. From this point of view, this system emerges thanks to home stimulation to numbers and frequency of exposition in formal schooling. Evidence during the last 5 years points to this last and controversial proposal (Lau et al., 2020; Lyons, Bugden, Zheng, De Jesus, & Ansari, 2018; Matejko & Ansari, 2016; Mussolin, Nys, Content, & Leybaert, 2014). In summary, the evidence of the problem argues in favor of an independent SNS from the ANS and, in fact, that learning the SNS impacts on ANS during the mapping process. In other words, learning numerical symbols refines the ANS as numerical representations become less approximate or more exact.
This research pursued two main objectives: (1) to add evidence on the symbol grounding problem by testing both causal hypothesis about the relation between SNS and ANS and (2) to study specific numerical cognitive processes underlying this relation between the two systems. In this sense, we hypothesized in favor of the Parallel Development Account (SNSàANS) and proposed that knowledge of the ordinal structure of the SNS would mediate the relation between both, what could be interpreted as ordinality explaining the transfer of exactness from SNS to ANS. Thus, 200 children in first year of preschool (4 to 5 years old) were followed during the academic year. Non-symbolic and symbolic comparison tasks and estimation tasks where applied at the beginning of the academic year (T1) and at the end (T2). Moreover, a cardinality task was administered in T1 and an ordinality task in T2, allowing to run two serial multiple mediator models to test both hypotheses with multiple longitudinal mediators. Results showed a bidirectional causal relation between ANS and SNS that was interpreted in support of the Parallel Development Account. Importantly, ordinality mediated de relation between SNS at T1 and ANS at T2, even controlling for the development of translation skills from SNS to ANS and cardinality.
This is the
first evidence showing that the knowledge of the relation between number
symbols, addressed by its ordinal structure, is the cognitive mechanism
underlying the refinement of the ANS, supporting the idea that they are systems
that develop independently.
NOTE: For references, please see References section on the manuscript.
Download preprint: psyarxiv.com/qwhzm/
Highlights
- The symbolic number system (SNS) emerges as an independent cognitive system than the approximate number system (ANS)
- The SNS refines the ANS during number learning
- Ordinal structure of the symbolic number system explains the refinement of the SNS on the ANS
- A bidirectional causal effect between the SNS and the ANS takes place at early preschool
How to cite
Peake, C., Briones, C., & Rodríguez, C. (2020, November 20). Ordinal structure of the symbolic number system mediates refinement of the approximate number system. https://doi.org/10.31234/osf.io/qwhzm